LeetCode每日一题(四月)
自从拿到 offer 后就没怎么刷题了,感觉还是得每天刷一下,正好四月一号,坚持打卡一下吧。
Day1 2810. 故障键盘
你的笔记本键盘存在故障,每当你在上面输入字符
'i'时,它会反转你所写的字符串。而输入其他字符则可以正常工作。给你一个下标从 0 开始的字符串
s,请你用故障键盘依次输入每个字符。返回最终笔记本屏幕上输出的字符串。
示例 1:
2
3
4
5
6
7
8
9
10
输出:"rtsng"
解释:
输入第 1 个字符后,屏幕上的文本是:"s" 。
输入第 2 个字符后,屏幕上的文本是:"st" 。
输入第 3 个字符后,屏幕上的文本是:"str" 。
因为第 4 个字符是 'i' ,屏幕上的文本被反转,变成 "rts" 。
输入第 5 个字符后,屏幕上的文本是:"rtsn" 。
输入第 6 个字符后,屏幕上的文本是: "rtsng" 。
因此,返回 "rtsng" 。示例 2:
2
3
4
5
6
7
8
9
10
11
12
输出:"ponter"
解释:
输入第 1 个字符后,屏幕上的文本是:"p" 。
输入第 2 个字符后,屏幕上的文本是:"po" 。
因为第 3 个字符是 'i' ,屏幕上的文本被反转,变成 "op" 。
因为第 4 个字符是 'i' ,屏幕上的文本被反转,变成 "po" 。
输入第 5 个字符后,屏幕上的文本是:"pon" 。
输入第 6 个字符后,屏幕上的文本是:"pont" 。
输入第 7 个字符后,屏幕上的文本是:"ponte" 。
输入第 8 个字符后,屏幕上的文本是:"ponter" 。
因此,返回 "ponter" 。提示:
1 <= s.length <= 100s由小写英文字母组成s[0] != 'i'
可以直接模拟,也能直接过,看到题解用的双端队列,思路不错,学习一下。
事实上,当字符串进行反转后,在末尾添加字符等价于「不对字符串进行反转,并且在开头添加字符」。因此,我们可以使用一个双端队列和一个布尔变量 head 来维护答案:
当遇到非 “i” 的字符时,如果 head 为真,就在队列的开头添加字符,否则在队列的末尾添加字符;
当遇到 “i” 时,将 head 取反。
head 的初始值为假。这样一来,每一个字符只需要 O(1) 的时间进行处理。
当处理完所有的字符后,如果 head 为真,那么将队列中的字符反序构造出答案字符串,否则正序构造出答案字符串。
1 | class Solution { |
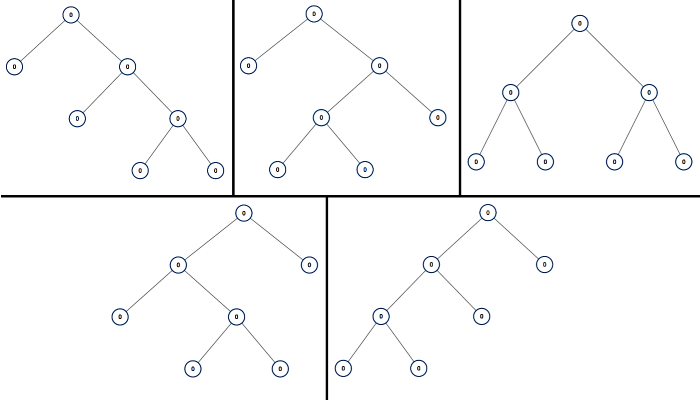
Day2 894. 所有可能的真二叉树
给你一个整数
n,请你找出所有可能含n个节点的 真二叉树 ,并以列表形式返回。答案中每棵树的每个节点都必须符合Node.val == 0。答案的每个元素都是一棵真二叉树的根节点。你可以按 任意顺序 返回最终的真二叉树列表。
真二叉树 是一类二叉树,树中每个节点恰好有
0或2个子节点。示例 1:
2
输出:[[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]示例 2:
2
输出:[[0,0,0]]提示:
1 <= n <= 20
刚看到题目感觉有点难度,看了题解发现也不是特别难
方法一:分治
根据题意可知,真二叉树中的每个结点的子结点数是 0 或 2,此时可以推出真二叉树中的结点数 n 为奇数,可以使用数学归纳法证明:
当真二叉树中只有
1个结点时,此时1为奇数,树中唯一的结点是根结点。当真二叉树中有
n个结点时,根据真二叉树的定义,此时可将其中一个叶结点增加两个子结点之后仍为真二叉树,新的真二叉树中有n + 2个结点,由于n是奇数,此时n+2也是奇数。
由于真二叉树中的结点数一定是奇数,因此当给定的节点数n 是偶数时,此时无法构成真二叉树,返回空值即可。当真二叉树节点数目 n 大于 1 时,此时真二叉树的左子树与右子树也一定为真二叉树,则此时左子树的节点数目与右子树的节点数目也一定为奇数。
当 n 是奇数时,n 个结点的真二叉树满足左子树和右子树的结点数都是奇数,此时左子树和右子树的结点数之和是 n−1,假设左子树的数目为i,则左子树的节点数目则为 n−1−i,则可以推出左子树与右子树的节点数目序列为:
$$
[(1,n−2),(3,n−4),(5,n−6),⋯ ,(n−2,1)][(1, n - 2), (3, n - 4), (5, n - 6), \cdots, (n - 2, 1)]
$$
假设我们分别构节点数目为i 和节点数目为n−1−i 的真二叉树,即可构造出 n 个结点的真二叉树。我们可以利用分治来构造真二叉树,分治的终止条件是 n=1。
当 n=1 时,此时只有一个结点的二叉树是真二叉树;
当 n>1 时,分别枚举左子树和右子树的根结点数,然后递归地构造左子树和右子树,并返回左子树与右子树的根节点列表。确定左子树与右子树的根节点列表后,分别枚举不同的左子树的根节点与右子树的根节点,从而可以构造出真二叉树的根节点。
1 | /** |
方法二:动态规划
上述同样的解题思路,我们还可以使用自底向上的动态规划。我们可以先构造节点数量为 1 的子树,然后构造节点数量为 5 的子树,然后依次累加即可构造出含有节点数目为 n 的真二叉树。
- 节点数目序列分别为 $[(1,1)]$ 的子树可以构造出节点数目
3的子树; - 节点数目序列分别为 $[(1,3),(3,1)]$ 的子树可以构造出节点数目
5的真二叉树; - 节点数目序列分别为 $[(1,5),(3,3),(5,1)]$ 的子树可以构造出节点数目
7的真二叉树; - 节点数目序列分别为 $[(1,i-2),(3,i-4),\cdots,(i-2,1)]$ 的子树可以构造出节点数目
i的真二叉树;
如果构造节点数目为n 真二叉树,此时可以从节点数目序列为 $[(1,n-2),(3,n-5),\cdots,(n-2,1)]$ 的真二叉树中构成,按照所有可能的组合数进行枚举,即可构造成节点数目为 n 的真二叉树。
1 | class Solution { |
Day3 1379. 找出克隆二叉树中的相同节点
给你两棵二叉树,原始树
original和克隆树cloned,以及一个位于原始树original中的目标节点target。其中,克隆树
cloned是原始树original的一个 副本 。请找出在树
cloned中,与target相同 的节点,并返回对该节点的引用(在 C/C++ 等有指针的语言中返回 节点指针,其他语言返回节点本身)。注意:你 不能 对两棵二叉树,以及
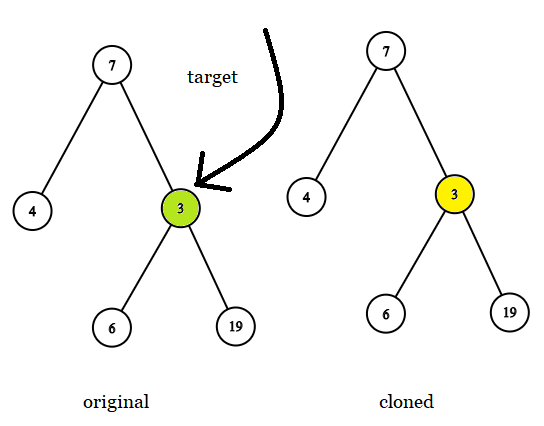
target节点进行更改。只能 返回对克隆树cloned中已有的节点的引用。示例 1:
2
3
输出: 3
解释: 上图画出了树 original 和 cloned。target 节点在树 original 中,用绿色标记。答案是树 cloned 中的黄颜色的节点(其他示例类似)。示例 2:
2
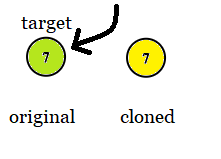
输出: 7示例 3:
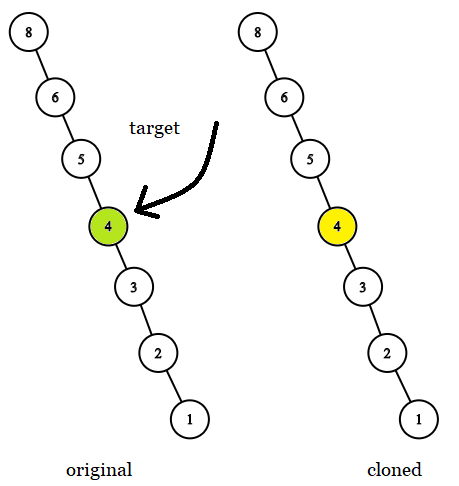
2
输出: 4提示:
- 树中节点的数量范围为
[1, 104]。- 同一棵树中,没有值相同的节点。
target节点是树original中的一个节点,并且不会是null。进阶:如果树中允许出现值相同的节点,将如何解答?
简单的遍历题,一开始没怎么看懂要求
1 | /** |
- Title: LeetCode每日一题(四月)
- Author: LoftyDust
- Created at : 2024-04-01 18:17:55
- Updated at : 2024-05-18 12:03:31
- Link: https://loftydust.top/a3def555d8f6.html
- License: This work is licensed under CC BY-NC-SA 4.0.